A Black Hole on the Desk

How would a black hole look like if it would be placed on a desk in a room? Disregarding the devastating destruction caused by the gravitational pull, what optical effects are caused by the intense gravity of a black hole?

This simulation shown here was one of the first computer-generated renderings of curved space revealing the details of a black hole’s optical effects.

Both images show a complex scenery, which should enable the viewer to get some intuitive feeling for the curvature of space, which is, according to Einsteins theory of General Relativity, caused by the existence of mass. The “Newtonian simulation” shows a view over the sea and a spherical mass hovering above it with a soccerball-like shape. Its gravitational force attracts the water below and creates a tiny hill of water. The arising ‘drop’ is just under this mass. Diagonally pointing to the backside there is a white bar, which should clearify the spatial context of the objects. The backward end of this bar hits a ikosaeder, which is shining in red light. This light also enlightens the backside of the spherical mass; this effect is partially visible on the sphere’s right side. Further behind at the distance of the brick cylinder with its flattened balls of gold there resides the tilted cylinder with its black and red colored surface. The influence of the curvature of space on this scene will be described detailed in the following text.

Note that the small colored sphere of the newtonian scenery has been removed from the scene in the einsteinian simulation, because the visual effect became too much otherwise.

The effect of Gravitational Lensing

It’s the basic idea of the Theory of General Relativity that mass will change space curvature and therefore light rays will follow another path than in flat (euclidean) space. As the path of a fast moving particle is bent by some massive object, light rays move “around a mass”.

The most simple case is known as the Schwarzschild-Solution, which describes the vacuum field of a spherical symmetric, nonrotating and uncharged amount of mass. It is a particularity of this solution to have an event horizon, if the source mass is concentrated within the Schwarzschild-Radius

An event horizon is the border of some special region; which can be crossed only in one direction – everything may get in, but nothing is able to get out. No event happening inside the event horizon may be get known in the outside – the inner region is therefore called to be “causally decoupled”. With real objects like stars or planets such phenomenas do not exist, since their masses cover a region which is by far greater then the region enclosed by the corresponding event horizon – e.g. the sun would have to shrink to a diameter of 2.5km, the earth itself to 0.8cm, otherwise an event horizon does not come into existence. Nevertheless any mass can be described formally as a length using the Schwarzschild-Radius according to the formula shown above. The simulation, which is presented here, makes use of a mass with a corresponding Schwarzschild-Radius of 0.5 meters and is seen from a distance of 25 meters.

A ray of light is bent by some mass with a Schwarzschild-Radius by an angle , where b denotes the minimal distance of the ray to the bending mass:

A mass, which effects are big enough to bend light, is therefore called an Gravitational Lens. The bending of light gets stronger, if the distance of the ray to the lens gets lesser:

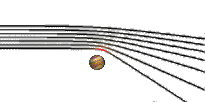
This behaviour is completely different as it is known with “normal” (optical) lenses of positive focal length made of glass; in that case, light is bent stronger if the ray’s distance to the optical axis gets greater:

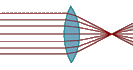
Also a glass lens with negative focal length does not behave like a gravitational lens, since light becomes focussed somehow in the gravitational field. Obviously gravitational lenses have some completely distinct, fundamentally othershaped mapping than usual optical lenses. It was the aim of this project to demonstrate this.

Its one unusual property that some object may be seen by an observer more tha once, e.g. the shining ikosaeder or the brick cylinder with its flattened golden balls; this effect may be imagined easy, since light rays may reach the observer’s eye using different paths:

In the case shown here the upper path is shorter than the lower one, the object seems to be less away seen by the upper path and therefore shines more brightly. This is clearly seen with the mapping of the ikosaeder, the right image is someone distorted to the “outer side”, but has nearly the same brightness as the object itself. Not so the counter image: residing on the opposite side of the gravitational lens, it is much smaller and less bright. Additionally, the counter image is reversed as in a mirror, which is especially obvious by the desk carrying the ikosahedron:

There is a special angle, some kind of “radius of inversion”, which determines the border of mirrored and normal, though distorted, images. Outside of this radius of inversion light rays are moved away from the lens, the images therefore are positioned to a greater distance to the gravitational lens than in a flat space (compare the image positions of the brick cylinder and the ikosaeder). Inside of the radius of inversion all objects visible outside may be seen another time – but now their images are smaller and reversed. The light using this path is not only bent a bit, but it makes “a trip around the mass”.

If there is an object exactly behind the gravitational lens, then there are no more two images (“inside” and “outside”), but both images get molten to a ring with the gravitational lens in its center. This phenomena is also known as the Ring of Einstein and has been observed in nature (at least approximative). The oberver now resides quasi in the “focus” of the lens, one point on the object’s surface is visited as a lineshape image and therefore maximally enlarged. In this simulation this object point is part of the tilted black and red sprinkled cylinder; the simulation also shows, that continuos surface structures are distorted more and more, the nearer they come to the inversion radius – until they finally become formed like the inversion radius itself and construct the Einstein Ring.

All these phenomenas, which are connected to the Einstein Ring, have already been observed in nature, although their scale is much smaller; Beams are bent by some degrees in this simulation, but modern astronomical observations show a typical scale of 15 arc seconds.

Another interesting effect, which benefits from the spatial structure of the scene depicted here, may be seen with the desk of wood, which is used as fundament for the icosahedric light source: Controversary to the newtonian simulation, where only the upper side of the desk is visible, the curvature of space also enables the observer to have a glimpse to the left edge of the downward side, where the curvature is stronger than on the right edge. Light originating from the downward side is bent by the gravitational active mass upwards and therefore may reach the observer’s eye. The desk itself seems to be totally distorted, though it is absolute plane in its real position as it was before in the newtonian simulation.

The Event Horizon

The event horizon can’t be visible itself, since no light may escape to outside from there. Nethertheless one may imagine the event horizon as surrounded by a thin membrane, which may send light to the outside world. The light originating from this membrane therefore enables the observer to catch some impressions from the space just outside the event horizon. In reality any light would become extremely reddened due to the gravitional field, so that the surface structure of the membrane could merely be seen in red or infrared light (and therefore possibly become unvisible). The gravitational redshift was explicitely excluded in this simulation because of this effect. However infalling lights gets blueshifted at the same amount as outcoming light becomes redshifted, such that these two effects just cancel for a static surface. So when only reflected light is taken into account (i.e. not a star but an planet), this simulation is correct regarding this aspect. But this is valid only if the surface under consideraton reflects light to the same amount at all wavelengths – otherwise there still would be color shifts occuring. In the most extreme case white light would arise at an object’s surface as X-rays or even gamma rays, and even if any reflected light would be visible by an outside observer as white light, the object itself would disappear because most material becomes transparent at X-ray or gamma ray wavelengths.

Near the event horizon there are phenomenas, which are completely unusual: controversely to great distances, where the path of light rays may rawly be described by hyperbolas, this approximation is no longer valid at smaller distances. There the light rays may be bent in such a strong kind, that it turns back to the light source, or, expressed in another way, the observer may spectate himself. At less distances to the event horizon there is a region, there the light may encircle the Black Hole or even get stuck in an orbit (the so-called “photon orbit“). The more the observer’s view direction approximates this photon orbit, the more often (and smaller) the whole outer world is been mapped spherically, additionally to the effects of gravitational lensing mentioned above.

Finally, looking inside the photon orbit, all light rays are bent so strong that they unavoidable touch the “surface” of the Black Hole (the covering membrane). Outer rays are slowly spiralling inwards, orbiting the Black Hole more than once, whereas rays, which are aimed directly to the Black Hole’s center, hit the surface nearly without bending. The Black Hole’s side lying in front of the observer therefore seems to be visible nearly without distortions, but soon one will become aware, that also the “north pole” of the ball is visible (as is the south pole, but this one is without light and therefore to dark to be seen). The light (equivalent to the view path of the observer) quasi spirals from the top down to the pole and beyond to the backside. Now also the part of the ball, which is enlightened by the red ikosaeder from behind, becomes visible – the observer is able to see not only one side of the black hole (as it is known from experience), but he may see the whole surface area!

This might be unusual enough, but additionally the whole surface is not only visible from one point of view, but from any point of view!

More about Black Holes is available on the page of the `Black Earth‘ (1997)

The calculations presented here were done in March 1993 on the workstations of the EDV-Pool at the University of Innsbruck. The Einsteinian simulation required seven hours to complete in a parallelized raytracing program on three HP-workstations – extrapolated to a PC’s power, a 386/33 MHz PC – the common commodity hardware at this time – would have required about two months to perform this computation of a single image. At the first update of this page in 1997 – when the Black Earth image series were created – such images could be rendered in a few minutes on a PC. On its next page update in 2009 raytracing of black holes could already be performed in real time within a fraction of second. By 2019, this now nearly ancient page got finally modernized into WordPress as part of the gravity.photon.at Website.

This information has also been published in
Relativity and Scientific Computing :… F.W.Hehl, R.A.Puntigam, H.Ruder (Eds.)
Relativity and Scientific Computing
Computer Algebra, Numerics, Visualization
ISBN 3-540-60361-1 Springer Verlag Berlin Heidelberg New York