Forming Black Holes Without Matter
Is matter required to form black holes? No. Pure vacuum can do that, too.
Gravitation is caused by mass, mass is equivalent to energy, Gravitational energy itself thus has a mass equivalent – even in pure vacuum, with no matter involved, as the mere curvature of spacetime itself can “store” energy just like a rubber band. “Brill Waves” (named after Dieter Brill, 1959, see (gr-qc/9302023) for a review) are an artificial construction of a spacetime with a high concentration of gravitational energy in a confined region at a specific instant in time. If this concentration of gravitational energy is sufficiently large, then the gravitational energy gets “stuck” as it forms a black hole. Such a Brill wave is called “supercritical”. In contrast, a “sub-critical” Brill waves contains gravitational energy that just dissipates into space over time, leaving nothing but flat empty spacetime.
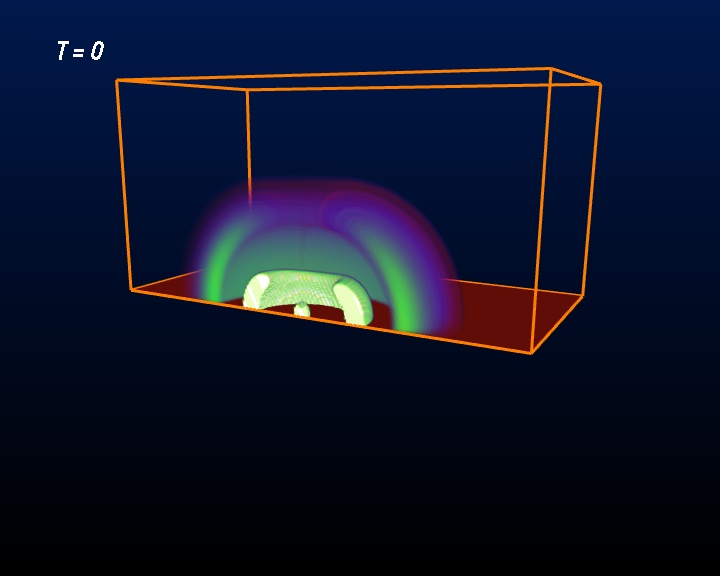
Initial Brill Wave 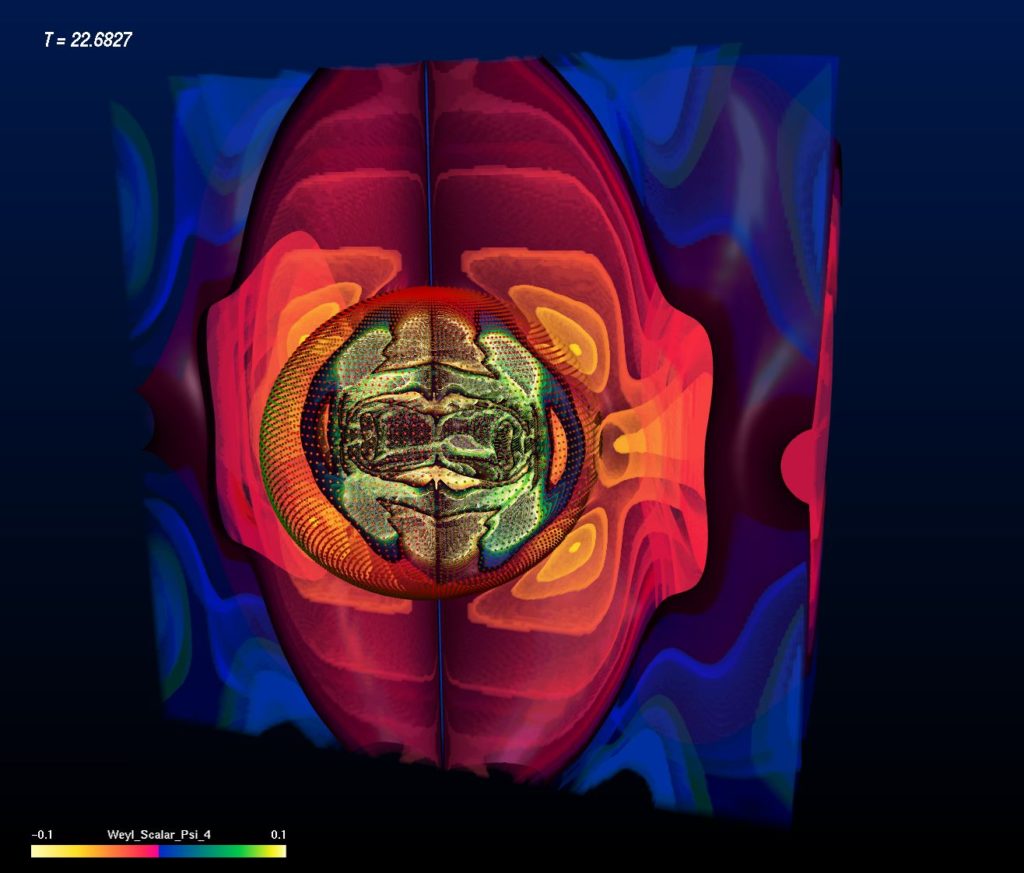
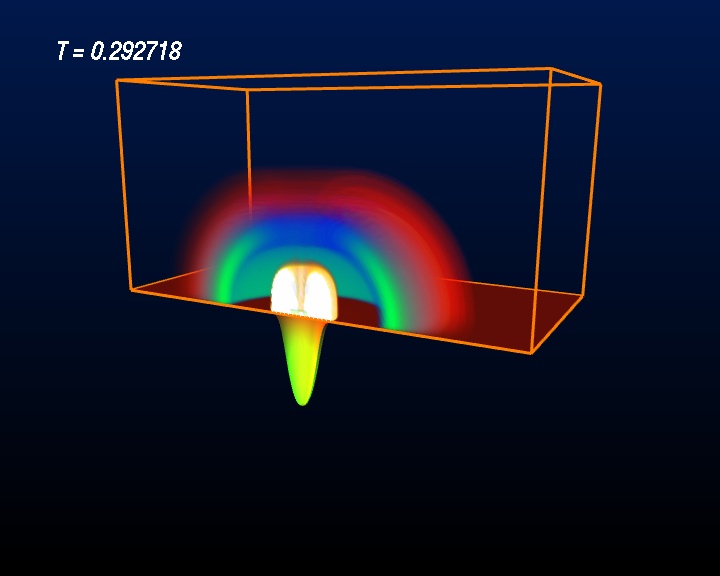
Super-critical Brill Wave with Horizon
[column-half-1]
Sub-Critical Brill Wave
Collapses under its own gravitiy, but bounces back and dissipates into space.
[/column-half-1]
[column-half-2]
Super-Critical Brill Wave
Collapses and “gets stuck” by forming a black hole. An Event horizon occurs after some time.
[/column-half-2]
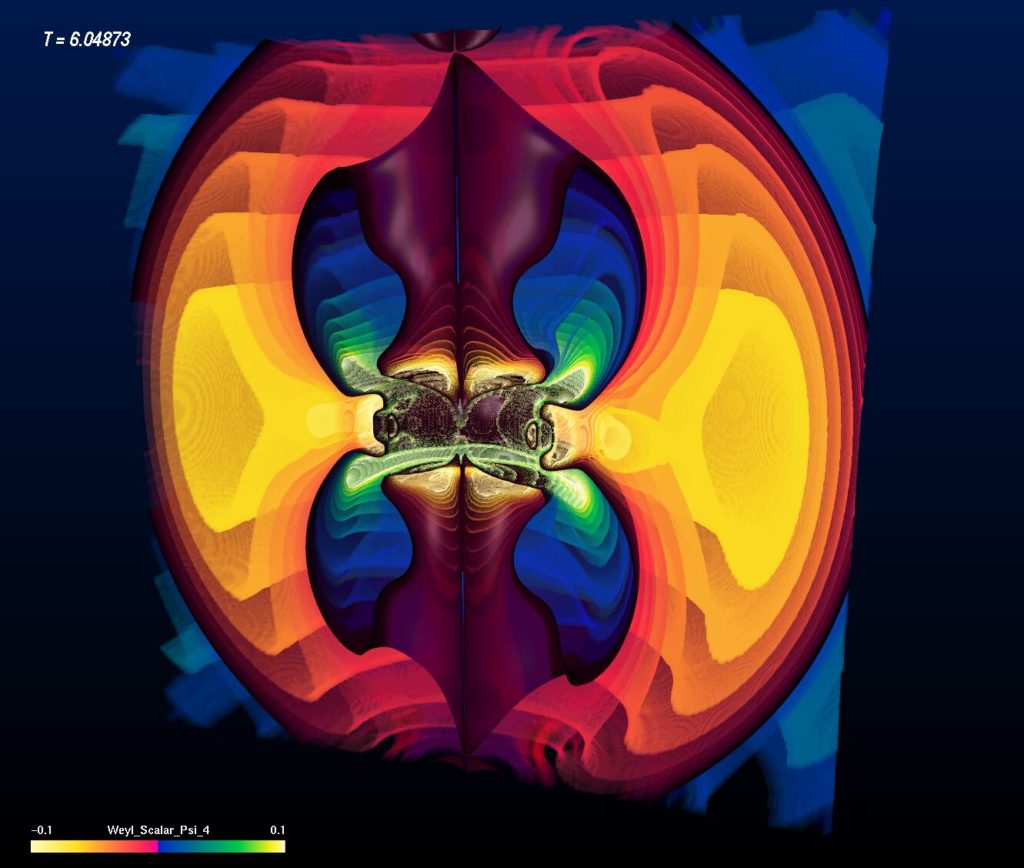
Evolution of a Sub-Critical Brill Wave
A sub-critical Brill Wave starts off from a concentrated amount of gravitational energy. At first it collapses “under its own weight”, but then bounces back and dissipates. Shown is the real part of the Ψ4 field with time shown below as height in a quartant of the volume (the scenario is symmetric), same quantity as used for the black hole merger visualizations. The “bottom surface” of the bounding box indicates the evolution of time, meaning that time runs slower the lower the surface gets. This resembles the property of black holes where time “gets stuck” at the event horizon as seen from an outside observer. Similarly, here time gets delayed due to the strong gravitational field under the momentary collapse, but it “recovers” to “flat spacetime” once the energy has dissipated. Watch the video referenced at the end of this page to see the full evolution.
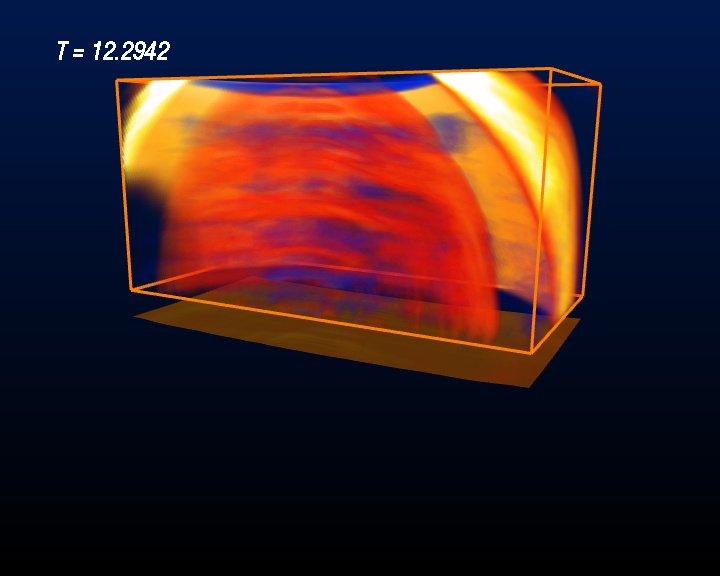
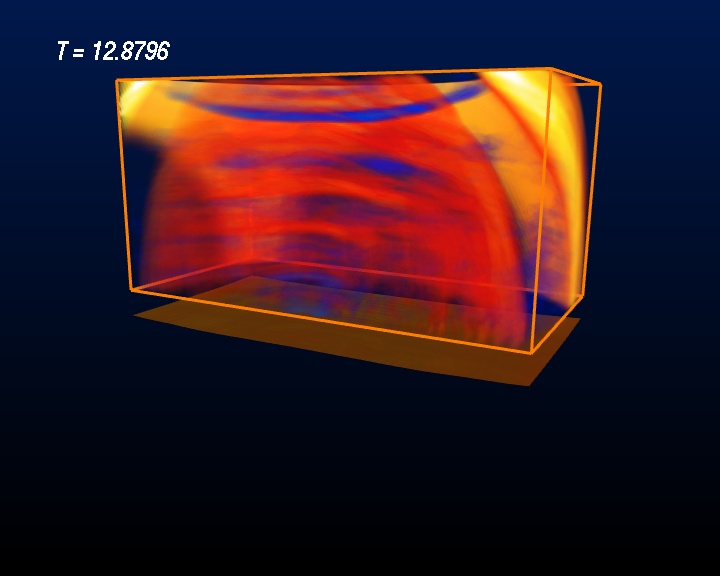
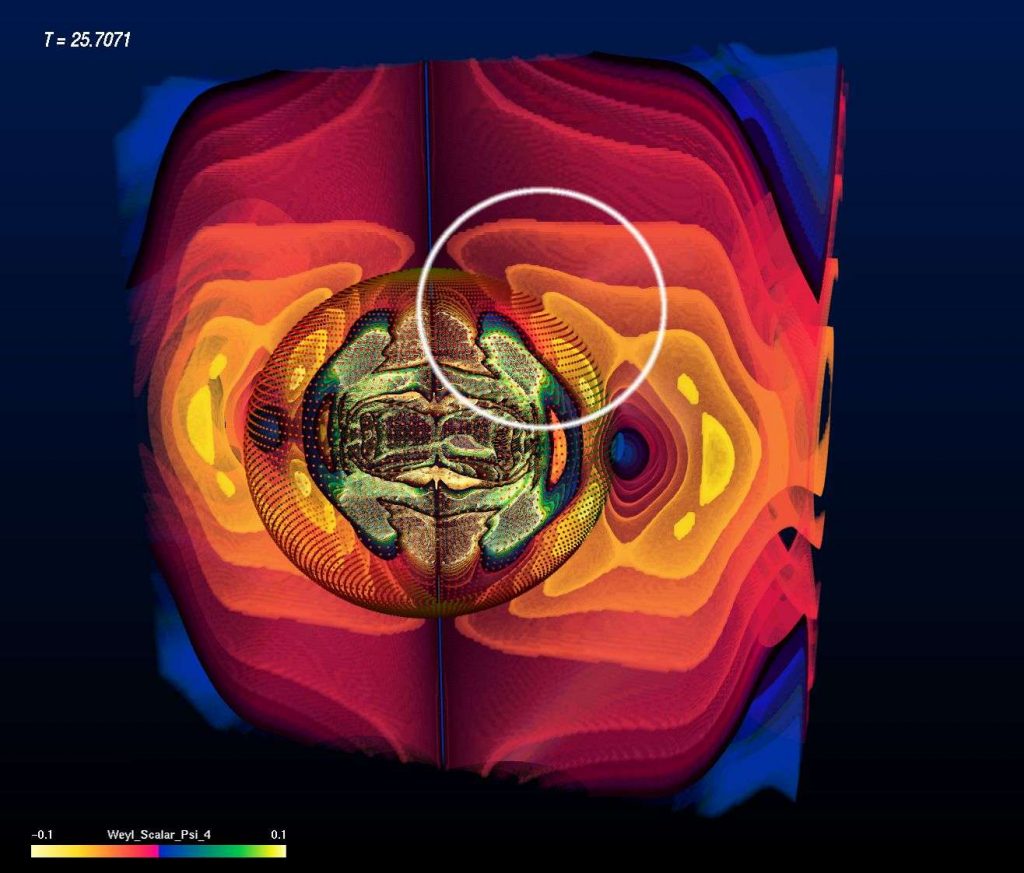
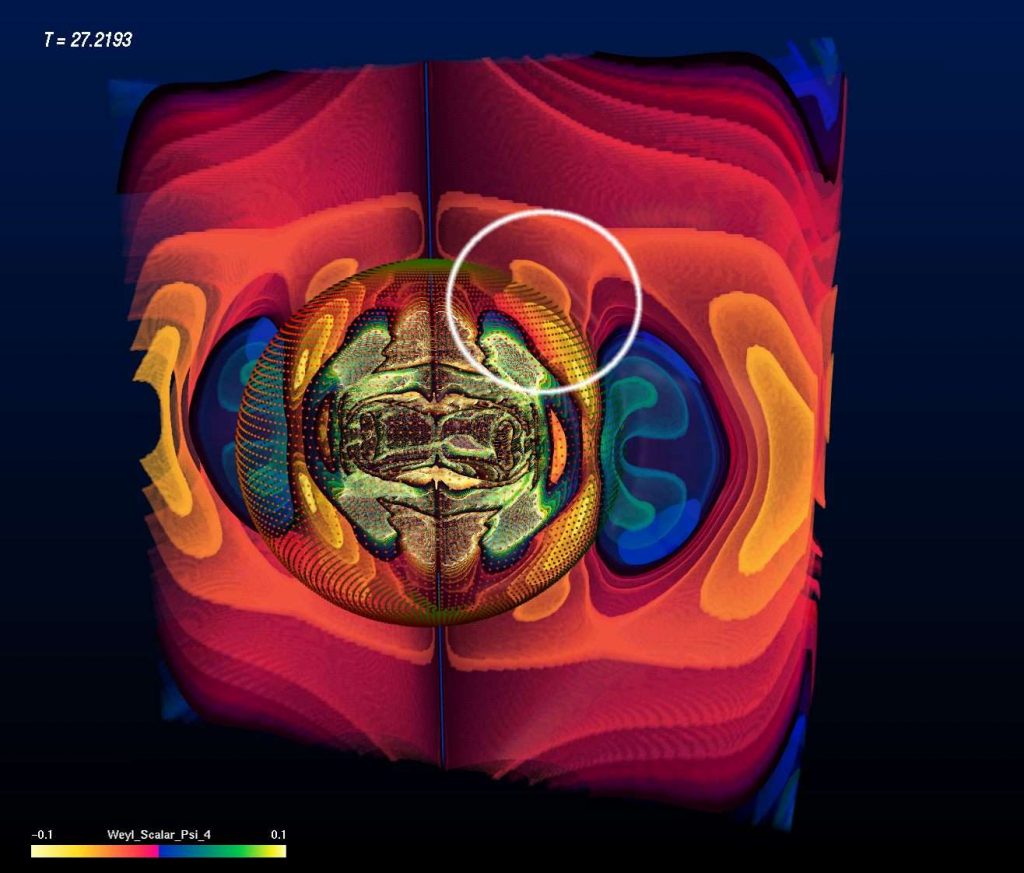
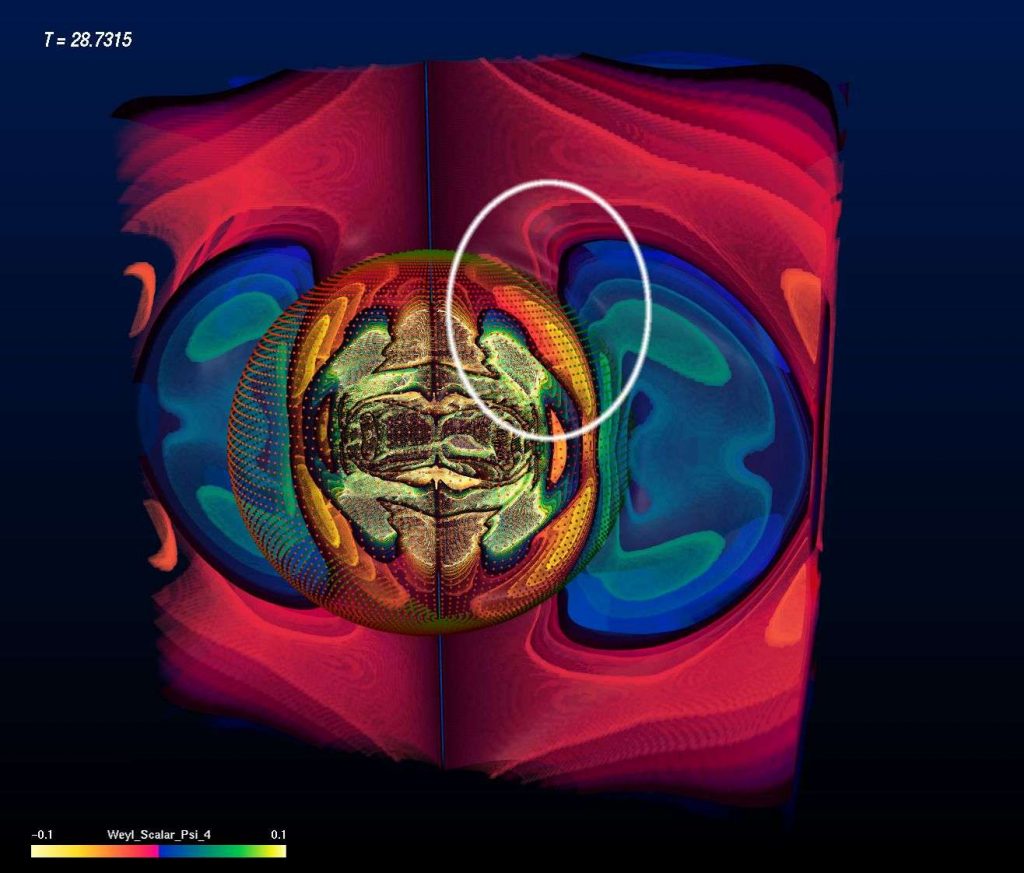
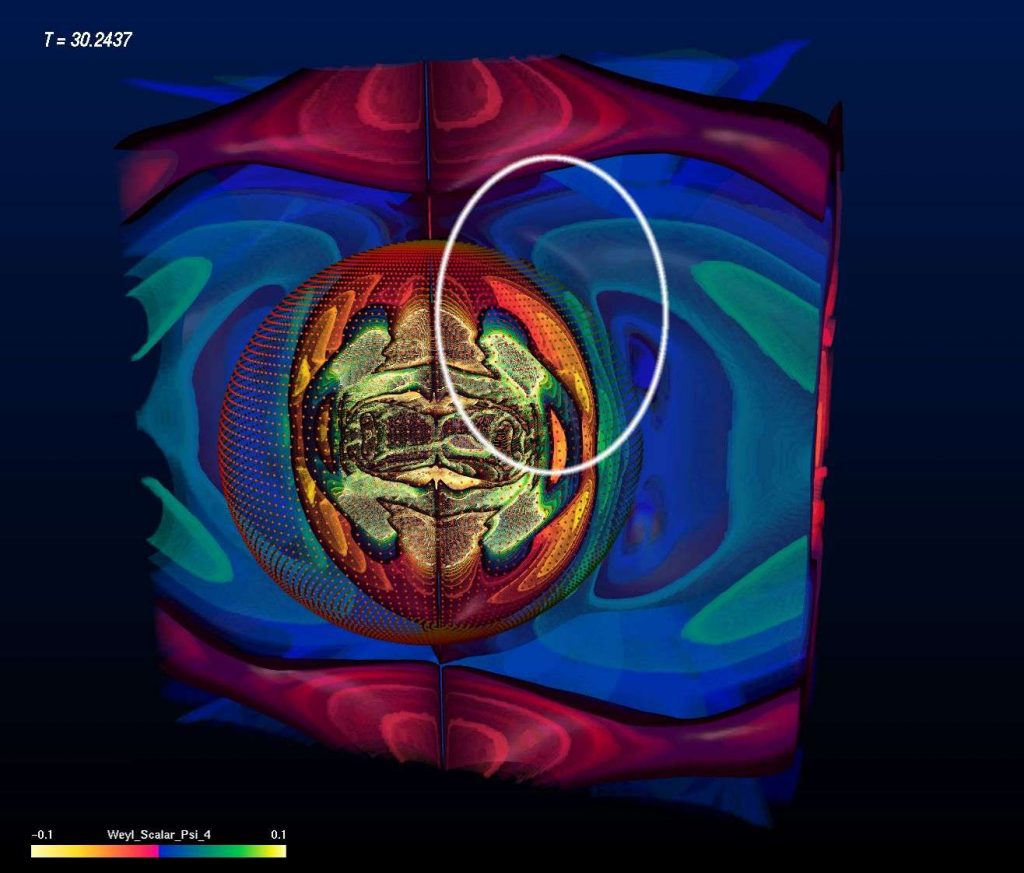
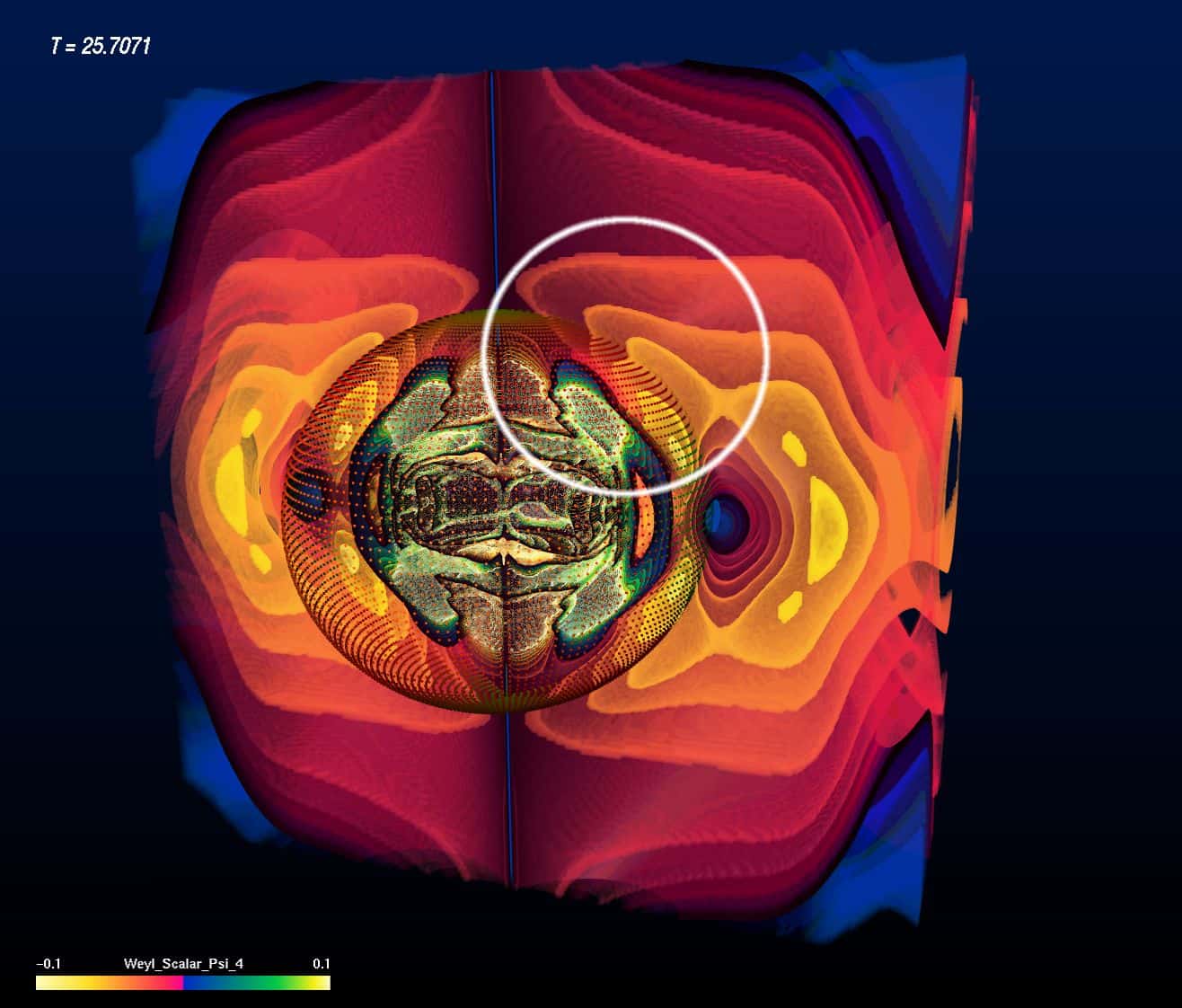
Evolution of a Super-Critical Brill Wave
A super-critical Brill Wave starts off with a concentrated amount of gravitational energy, but higher concentration than the sub-critical Brill Wave. In this case the Brill Waves “gets stuck”, meaning that only part of the initial gravitational energy is radiated away while the remaining part remains within a confined region and never escapes. In other words, a black hole is formed. The image sequence shown below depicts the intensity levels of the Re Ψ4 field in a half-space (bitant, or double Quartant). Red is the positive part, blue the negative part. Pay attention to the particular features of the Ψ4 field: While some features still run outwards – like in the sub-critical case – some other features are running inwards. The boundary between features running inwards and running outwards is the event horizon of the black hole! Determining the event horizon numerically is a major computational challenge. The dotted surface shown in the images depicts the location of an “apparent horizon”, which is an indicator for the event horizon that is easier to compute. An apparent horizon is known to reside inside an event horizon – thus the existence of an apparent horizon hints at the existence of an event horizon further out. And indeed, in these images we can see the boundary of features “running inwards” and “running outwards” just a bit outside of the apparent horizon.
Indispensability of Numerical Relativity
While the theoretical existence of sub-critical and super-critical Brill Waves – those that are not a black hole and those that are black holes right from the beginning – has been known from analytical computations, it was unclear whether an initially sub-critical Brill Wave (containing no Black Hole) may become super-critical later on (i.e., forming a black hole from a non-black hole status). Analytically this situation could not be investigated. Only numerical simulations (gr-qc/9904013) are able to show that this situation is indeed possible: From a spacetime made out of pure gravitational energy (i.e., a matter-free vacuum) a black hole can be formed which at the end cannot be distinguished from a black hole formed from matter because only its mass can be observed from the outside.
Animation Sequences
The visualizations presented on this page were made 1999 as part of the AEI-ZIB cooperation project based on the data leading to the article (gr-qc/9904013) .
Violation of Mach’s Principle
Even though Mach’s principle was hugely inspiring Einstein’s theory of general relativity, it eventually turned out that GR is violating it: Brill Waves provide a prominent example. Mach envisioned that the matter in the universe “defines” the frame of motion, particularly rotational motion such that rotation is “relative to the surrounding matter”, thereby dropping the Newtonian concept of an “absolute space” that defines what rotates and what not. GR has demonstrated that indeed rotating matter causes non-Newtonian effects on orbiting objects. However, as Brill Waves demonstrate, no matter is required at all to cause such space-time effects (the inertio-gravitational field): black holes may form from pure vacuum, and any rotational component (e.g. caused by two black holes merging) would cause the exactly same effects on orbiting objects. Thus, the inertio-gravitational field is determined even in a completely matter-free spacetime – a situation that Einstein (who died before Brill published his thesis 1959) did not anticipate.
The difference between black holes formed from matter or from gravitational energy is particularly peculiar because gravitational energy cannot be localized: At each point in space an observer would only detect vacuum, which is even locally flat space, whereas for matter an observer could measure a local density (of gas, of particles, of electro-magnetic energy, …) . It is thus not possible to determine “how much gravitational energy” is located at a specific point. Only when studying a region from a distance it is possible to assign it some asymptotic mass.