机の上にブラックホールがあったら？

部屋の机の上にブラックホールがあったらどんな風に見えるだろうか？引力によって生じる壊滅的な破壊を考慮しない場合, ブラックホールの強い重力によって生じる光学効果はどんなものだろう?

ここに示すシミュレーションは，ブラックホールの光学効果を詳細に示した，曲がった空間を初めてコンピュータで再現したものの１つです.

二つの画像ともに show 複雑な光景を, which should enable the viewer to get 空間の歪みに対するいくつかの直感的な感覚を, which is, アインシュタインの一般相対性理論によると, 質量によって生じる. “ニュートンシミュレーション” shows 海の上 and 球状の物質 hovering above it with サッカーボールのような形. その重力は下の水をひきつけて小さな水の丘を作っている． 発生している ‘滴’ はちょうどこの物質の下にある. Diagonally pointing to the backside there is a white bar, which should clearify the spatial context of the objects. このバーの後退端は， 赤く輝いている二十面体にあたっている. この光は， also enlightens the backside of the spherical mass; この効果は，部分的に球の右側で見られる。Further behind at the distance of the brick cylinder with its flattened balls of gold there resides 傾いた cylinder with 赤色と黒色の表面. このシーンにおける空間の歪みの影響は ，これ以降に詳細に述べます.

ニュートンシミュレーションでの小さなカラー球はアインシュタインシミュレーションのシーンからは除かれていることに留意してください． なぜならば，そうしないと 視覚的な効果が非常に大きくなってしまうからです.

重力レンズ効果

一般相対性理論(the Theory of General Relativity)の基本的な考えは， that 質量が空間の歪みを変えるだろう，and それゆえ 光線(light rays) will follow another path than in flat (euclidean) space. As the path of a fast moving particle is bent by some 重い object, 光線は”塊のまわりを”移動します.

最もシンプルなケースは is known as the シュヴァルツシルト解 , which describes the vacuum field of 球対称, nonrotating and uncharged amount of mass. It is a particularity of this solution to have an event horizon, if the source mass is concentrated within the Schwarzschild-Radius

事象の地平面(An event horizon)は いくつかの特別な領域の境界です。; which can be crossed only in one direction – everything may get in, but nothing is able to get out. No event happening inside the event horizon may be get known in the outside – the inner region is therefore called to be “causally decoupled”. With real objects like stars or planets such phenomenas do not exist, since their masses cover a region which is by far greater then the region enclosed by the corresponding event horizon – 例えば， 太陽は 直径2.5 kmまで小さくなるし, 地球は直径0.8 cmになる, さもなければ，事象の地平面は存在しなくなる. Nevertheless any mass can be described formally as a length using 上記に示す公式によるシュヴァルツシルト半径を使って. このシミュレーションは, ここに示す通り, makes use of a mass with a corresponding シュヴァルツシルト 半径 of 0.5 meters and is seen from 25 mの距離.

光線 is bent by some mass with a シュヴァルツシルト半径 by an angle , where b denotes the minimal distance of the ray to the bending mass:

物質は, which 効果が光を曲げるほど十分に大きい, is それゆえ重力レンズと呼ばれる. 光の曲がりはより強くなっていく, if the distance of the ray to the lens gets lesser:

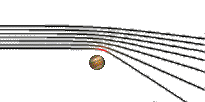
このふるまい is completely different as it is known with “通常の” (光学的な) lenses of 正の焦点距離 made of glass; in that case, 光は強く曲がる if the ray’s distance to the optical axis gets greater:

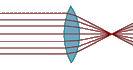
Also ガラスのレンズ with negative focal length does not behave like 重力レンズ, since light becomes focussed somehow in 重力場. 明らかに gravitational lenses have some completely distinct, fundamentally other shaped mapping than usual optical lenses. It was the aim of this project to demonstrate this.

Its one unusual property that some object may be seen by an observer more than once, e.g. the shining ikosaeder or the brick cylinder with its flattened golden balls; この効果は 簡単に想像されるかもしれない, since 光線は may reach the observer’s eye 異なる経路を使って:

ここで示すケースにおいては， 上方の通り道 is shorter than the lower one, the object seems to be less away seen by the upper path and therefore shines more brightly. This is clearly seen with the mapping of the 二十面体, the right image is someone distorted to the “outer side”, but has nearly the same brightness as the object itself. Not so the counter image: residing on the opposite side of the gravitational lens, it is much smaller and less bright. 加えて, the counter image is reversed as in a mirror, which is especially obvious by the desk carrying the ikosahedron:

There is a special angle, some kind of “radius of inversion”, which determines the border of mirrored and normal, though distorted, images. Outside of this radius of inversion light rays are moved away from the lens, the images therefore are positioned to a greater distance to the gravitational lens than in a flat space (compare the image positions of the brick cylinder and the ikosaeder). Inside of the radius of inversion all objects visible outside may be seen another time – but now their images are smaller and reversed. この通り道を使う光はわずかに曲がるだけではなく, but it makes “a trip around the mass”.

If there is an object exactly behind 重力レンズ, then there are no more two images (“inside” and “outside”), しかし 両方の画像は get molten to a ring with the gravitational lens in its center. この現象は is also known as アインシュタインリング and has been observed in nature (at least approximative). The oberver now resides quasi in the “focus” of the lens, one point on the object’s surface is visited as a lineshape image and therefore maximally enlarged. In this simulation this object point is part of the tilted black and red sprinkled cylinder; このシミュレーションは、また、 shows, that continuos surface structures are distorted more and more, the nearer they come to the inversion radius – until they finally become formed like the inversion radius itself and construct アインシュタインリング.

これらの現象の全ては, アインシュタインリングとつながっており, have already been observed in nature, although their scale is much smaller; Beams are bent by some degrees in this simulation, しかし 現代の天体観測は show a typical scale of 15 arc seconds.

もうひとつの興味深い効果は, which benefits from the spatial structure of the scene depicted here, may be seen with the desk of wood, which is used as fundament for the icosahedric light source: Controversary to the newtonian simulation, where only the upper side of the desk is visible, the curvature of space also enables the observer to have a glimpse to the left edge of the downward side, where the curvature is stronger than on the right edge. Light originating from the downward side is bent by the gravitational active mass upwards and therefore may reach the observer’s eye. 机自体は全体として歪んでいる, though it is absolute plane in its real position as it was before in the newtonian simulation.

事象の地平面

事象の地平面自体は， そこから外へ光が逃げていかないため見ることができない. Nethertheless one may imagine the event horizon as surrounded by a thin membrane, which may send light to the outside world. The light originating from this membrane therefore enables the observer to catch some impressions from the space just outside the event horizon. In reality any light would become extremely reddened due to the gravitional field, so that the surface structure of the membrane could merely be seen in red or infrared light (and therefore possibly become unvisible). The gravitational redshift was explicitely excluded in this simulation because of this effect. しかしながら infalling lights gets blueshifted at the same amount as outcoming light becomes redshifted, such that these two effects just cancel for a static surface. So when only reflected light is taken into account (i.e. not a star but an planet), this simulation is correct regarding this aspect. But this is valid only if the surface under consideration reflects light to the same amount at all wavelengths – otherwise there still would be color shifts occuring. 最も極端な例では， white light would arise at an object’s surface as X-rays or even gamma rays, and even if any reflected light would be visible by an outside observer as white light, the object itself would disappear because most material becomes transparent at X-ray or gamma ray wavelengths.

Near the event horizon there are phenomenas, which are completely unusual: controversely to great distances, where the path of light rays may rawly be described by hyperbolas, this approximation is no longer valid at smaller distances. There the light rays may be bent in such a strong kind, that it turns back to the light source, or, expressed in another way, the observer may spectate himself. At less distances to the event horizon there is a region, there the light may encircle the Black Hole or even get stuck in an orbit (the so-called “photon orbit“). The more the observer’s view direction approximates this photon orbit, the more often (and smaller) the whole outer world is been mapped spherically, additionally to the effects of gravitational lensing mentioned above.

Finally, looking inside the photon orbit, all light rays are bent so strong that they unavoidable touch the “surface” of the Black Hole (the covering membrane). Outer rays are slowly spiralling inwards, orbiting the Black Hole more than once, whereas rays, which are aimed directly to the Black Hole’s center, hit the surface nearly without bending. The Black Hole’s side lying in front of the observer therefore seems to be visible nearly without distortions, but soon one will become aware, that also the “north pole” of the ball is visible (as is the south pole, but this one is without light and therefore to dark to be seen). The light (equivalent to the view path of the observer) quasi spirals from the top down to the pole and beyond to the backside. Now also the part of the ball, which is enlightened 赤い正十二面体によって from behind, becomes visible – 観測者は able to see not only one side of the black hole (as it is known from experience), but he may see the whole surface area!

This might be unusual enough, but additionally the whole surface is not only visible from one point of view, but from any point of view!

More about Black Holes is available on the page of the `Black Earth‘ (1997)

ここで示す計算結果は were done in March 1993 on the workstations of the EDV-Pool インスブルック大学の. The Einsteinian simulation required seven hours to complete in a parallelized raytracing program on three HP-workstations – extrapolated to a PC’s power, a 386/33 MHz PC – the common commodity hardware at this time – would have required about two months to perform this computation of a single image. At the first update of this page in 1997 – when the Black Earth image series were created – such images could be rendered in a few minutes on a PC. On its next page update in 2009 raytracing of black holes could already be performed in real time within a fraction of second. By 2019, this now nearly ancient page got finally modernized into WordPress as part of the gravity.photon.at Website.

This information has also been published in
Relativity and Scientific Computing :… F.W.Hehl, R.A.Puntigam, H.Ruder (Eds.)
Relativity and Scientific Computing
Computer Algebra, Numerics, Visualization
ISBN 3-540-60361-1 Springer Verlag Berlin Heidelberg New York